Contoh: Matriks
-
- A =
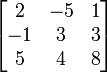 ditranspose menjadi AT =
ditranspose menjadi AT = 
- A =
Matriks
-
- B =
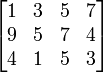 ditranspose menjadi BT =
ditranspose menjadi BT = 
- B =
Rumus-rumus operasi Transpose sebagai berikut:
-
- 1.

- 2.
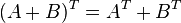 dan
dan 
- 3.
 dimana k adalah skalar
dimana k adalah skalar - 4.
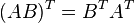
- 1.
All About Aljabar Linear Elementer
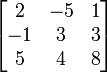 ditranspose menjadi AT =
ditranspose menjadi AT = 
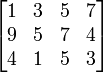 ditranspose menjadi BT =
ditranspose menjadi BT = 

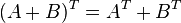 dan
dan 
 dimana k adalah skalar
dimana k adalah skalar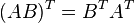



0 komentar:
Posting Komentar